整理：欧拉角与旋转矩阵

首先讨论二维平面坐标下的旋转，然后引申至三维。

1.1 平面二维旋转

如下图，XY坐标系中，向量OP旋转β角度到了OP’的位置：

根据三角函数关系，可以列出向量OP与OP’的坐标表示形式：

对比上面个两个式子，将第2个式子展开：
$$
\left{\begin{array}{l}
x{\prime}=|O P| \cdot \cos (\alpha+\beta)=|O P| \cdot(\cos \alpha \cdot \cos \beta-\sin \alpha \cdot \sin \beta)=x \cdot \cos \beta-y \cdot \sin \beta \
y{\prime}=|O P| \cdot \sin (\alpha+\beta)=|O P| \cdot(\cos \alpha \cdot \sin \beta+\sin \alpha \cdot \cos \beta)=x \cdot \sin \beta+y \cdot \cos \beta
\end{array}\right.
$$
其中：
$$
y=|OP|\cdot\sin \alpha \
x=|OP|\cdot\cos \alpha
$$
用矩阵表示：
$$
\left[\begin{array}{l}
x{\prime} \
y{\prime}
\end{array}\right]=\left[\begin{array}{cc}
\cos \beta & -\sin \beta \
\sin \beta & \cos \beta
\end{array}\right] \cdot\left[\begin{array}{l}
x \
y
\end{array}\right]
$$

三维旋转

• 绕Z轴

参照上面的图，添加一个Z轴，则上面的二维旋转实际上就是绕Z轴的三维旋转

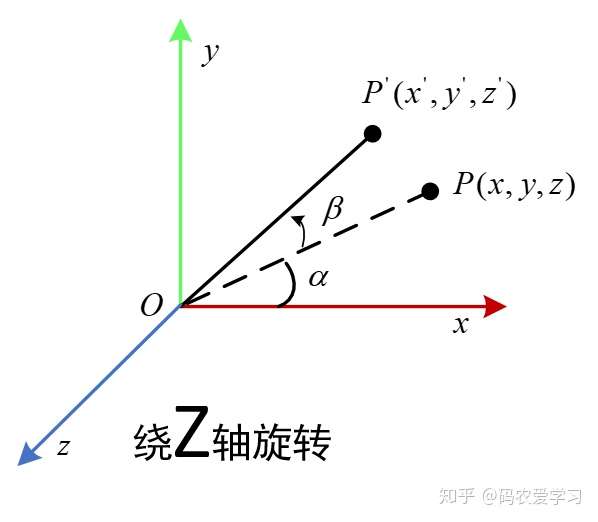
其中z的值始终不变：
$$
\left{\begin{array}{l}
x{\prime}=x \cdot \cos \beta-y \cdot \sin \beta \
y{\prime}=x \cdot \sin \beta+y \cdot \cos \beta \
z{\prime}=z
\end{array}\right.
$$
用矩阵关系表示：
$$
\left[\begin{array}{c}
x^{\prime} \
y^{\prime} \
z^{\prime}
\end{array}\right]=\left[\begin{array}{ccc}
\cos \beta & -\sin \beta & 0 \
\ \sin \beta & \cos \beta & 0 \
0 & 0 & 1
\end{array}\right] \cdot\left[\begin{array}{l}
x \
y \
z
\end{array}\right]
=\left[\begin{array}{c}
x \cdot \cos \beta-y \cdot \sin \beta \
x \cdot \sin \beta+y \cdot \cos \beta \
z
\end{array}\right]
$$
同理

用矩阵关系表示：
$$
\left[\begin{array}{c}
x^{\prime} \
y^{\prime} \
z^{\prime}
\end{array}\right]=\left[\begin{array}{ccc}
\cos \beta & \sin \beta & 0 \
0 & 1 & 0 \
-\sin \beta & \cos \beta & 0\
\end{array}\right] \cdot\left[\begin{array}{l}
x \
y \
z
\end{array}\right]
$$
绕x轴

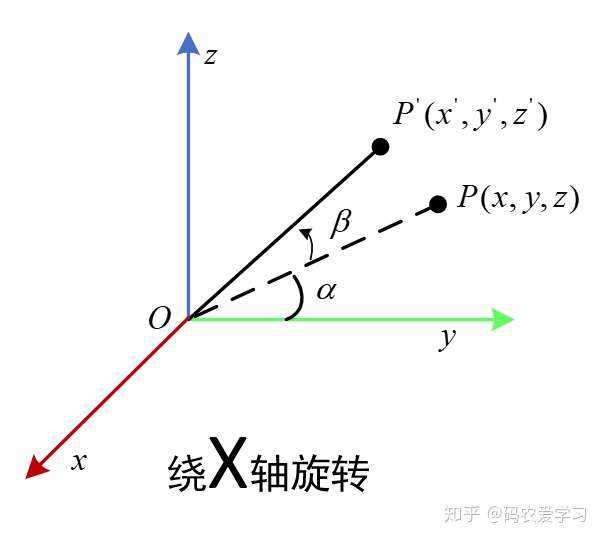
$$
\left[\begin{array}{l}
y^{\prime} \
z^{\prime} \
x^{\prime}
\end{array}\right]=\left[\begin{array}{ccc}
\cos \beta & -\sin \beta & 0 \
\sin \beta & \cos \beta & 0 \
0 & 0 & 1
\end{array}\right] \cdot\left[\begin{array}{l}
y \
z \
x
\end{array}\right] \Rightarrow\left[\begin{array}{l}
x^{\prime} \
y^{\prime} \
z^{\prime}
\end{array}\right]=\left[\begin{array}{lll}
1 & 0 & 0 \
\mid 0 & \cos \beta & -\sin \beta \
0 & \sin \beta & \cos \beta
\end{array}\right] \cdot\left[\begin{array}{l}
x \
y \
z
\end{array}\right]
$$

欧拉角与旋转矩阵

给出逆时针旋转的角度为正时（与右手系旋转方向相同的为旋转正方向），绕不同轴的旋转结果：
$$
R_{x}=\left[\begin{array}{ccc}
1 & 0 & 0 \
0 & \cos \theta & -\sin \theta \
0 & \sin \theta & \cos \theta
\end{array}\right], R_{y}=\left[\begin{array}{ccc}
\cos \phi & 0 & \sin \phi \
0 & 1 & 0 \
-\sin \phi & 0 & \cos \phi
\end{array}\right], R_{z}=\left[\begin{array}{cc}
\cos \psi & -\sin \psi & 0 \
\sin \psi & \cos \psi & 0 \
0 & 0 &1
\end{array}\right]
$$
假设有一个坐标系 b bb（其上有一个点 p pp（点和向量是空间中一样东西，只有当选取坐标系时才讨论它的的坐标），坐标也用 p pp 表示），它要绕X轴逆时针转 α αα 角度，那么在旋转之后的坐标系下点p的坐标（记为$p\prime$）变成了多少？做一下数学转换得到：
$$
R_{x} * p^{\prime}=p
$$
当从w系依次进行ZYX顺序的旋转得到b系，那么根据式(2)可得$R_{bw}$

$$
\begin{aligned}
R_{b w} &=R_{x}^{T} * R_{y}^{T} * R_{z}^{T} \
&=\left[\begin{array}{ccc}
1 & 0 & 0 \
0 & \cos \theta & -\sin \theta \
0 & \sin \theta & \cos \theta
\end{array}\right] *\left[\begin{array}{c}
T \
*
\end{array}\left[\begin{array}{ccc}
\cos \phi & 0 & \sin \phi \
0 & 1 & 0 \
-\sin \phi & 0 & \cos \phi
\end{array}\right]^{T} *\left[\begin{array}{ccc}
\cos \psi & -\sin \psi & 0 \
\sin \psi & \cos \psi & 0 \
0 & 0 & 1
\end{array}\right]^{T}\right.\
&=\left[\begin{array}{ccc}
1 & 0 & 0 \
0 & \cos \theta & \sin \theta \
0 & -\sin \theta & \cos \theta
\end{array}\right] *\left[\begin{array}{ccc}
\cos \phi & 0 & -\sin \phi \
0 & 1 & 0 \
\sin \phi & 0 & \cos \phi
\end{array}\right] *\left[\begin{array}{ccc}
\cos \psi & \sin \psi & 0 \
-\sin \psi & \cos \psi & 0 \
0 & 0 & 1
\end{array}\right]
\end{aligned}
$$

从w系变换到b系所进行的ZYX顺序的旋转的含义是什么呢？我们知道 $t_{w b}$是b系的坐标原点在w系下的坐标，那么此处的ZYX顺序的旋转就是指：b系在w系下的欧拉角，表示w系按照此欧拉角顺序旋转即可得到b系！既然是b系在w系下的欧拉角，那么我们求解的应该是$R_{wb}$，所以对$R_{bw}$做转置，得到$R_{wb}$，如下：
$$
\begin{aligned}
w b=R_{b w}^{T} &=R_{z} * R_{y} * R_{x} \
&=\left[\begin{array}{ccc}
\cos \psi & -\sin \psi & 0 \
\sin \psi & \cos \psi & 0 \
0 & 0 & 1
\end{array}\right] *\left[\begin{array}{ccc}
\cos \phi & 0 & \sin \phi \
0 & 1 & 0 \
-\sin \phi & 0 & \cos \phi
\end{array}\right] *\left[\begin{array}{ccc}
1 & 0 & 0 \
0 & \cos \theta & -\sin \theta \
0 & \sin \theta & \cos \theta
\end{array}\right]
\end{aligned}
$$
注意，此时的左乘顺序跟旋转顺序是相反的。同样，当从旋转矩阵$R_{wb}$转换成ZYX顺序的欧拉角时，此欧拉角也表示：b系在w系下的欧拉角，即从w系($R_{wb}$中的目标系)变换到b系（$R_{wb}$中的源坐标系）所用的欧拉角。

从旋转矩阵转换欧拉角时，将欧拉角转换成旋转矩阵使用的什么样的公式，那么从旋转矩阵转换成欧拉角的时候也要使用同一套公式，这样才不容易乱套。

旋转的本质

坐标系$b_1$（其上有一个点 $p$，坐标也用$p$表示），先绕X轴转$\alpha$角度，再绕Y轴转$\beta$，再绕Z轴转$\gamma$，得到$b_2$坐标系，计算$R_{b_2b_1}$？

将这个过程分为下面三步进行：

1. 坐标系$b_1$先绕$X$轴转$\alpha$，在新坐标系$b_1\prime$下的坐标为：
   $$
   p^{\prime}=R_{x}^{T} * p
   $$

2. 坐标系$b_1\prime$再绕Y轴转$\beta$ ，在新坐标系$b_1\prime\prime$下$p$的坐标：
   $$
   p^{\prime \prime}=R_{y}^{T} * p^{\prime}
   $$

3. 坐标系$b_1\prime\prime$再绕Z轴转$\gamma$，在新坐标系$b_1\prime\prime\prime$下$p$的坐标是：
   $$
   R_{b_{2} b_{1}}=R_{z}^{T} * R_{y}^{T} * R_{x}^{T}
   $$
   如果明白了上面的推导过程，以后所有的旋转都能这么推导，因为旋转是叠加的（在上次的结果上继续左乘）。假设存在这样的旋转，先绕X轴转$\alpha$角度，再还是绕X轴转$\alpha\prime$,再绕Y轴转$\beta$，然后还是绕X轴转$\alpha\prime\prime$
   ′′
   ，整个旋转下来组合的旋转矩阵就是：

$$
R=R\left(\alpha^{\prime \prime}\right)^{T} * R(\beta)^{T} * R\left(\alpha^{\prime}\right)^{T} * R(\alpha)^{T}=R\left(\alpha^{\prime \prime}\right)^{T} * R(\beta)^{T} * R\left(\alpha^{\prime}+\alpha\right)^{T}
$$

之所以$\alpha$与$\alpha\prime$能合并是因为他俩的旋转轴相同！